Miles H. Wheeler

I am a Lecturer (Assistant Professor) in Analysis in the Department of Mathematical Sciences at the University of Bath. Before coming to Bath, I was a University Assistant at the Faculty of Mathematics at the University of Vienna, and before that I was a postdoc at the Courant Institute of Mathematical Sciences supported by an NSF fellowship. I am interested in nonlinear partial differential equations, and in particular in overdetermined elliptic boundary value problems coming from fluid mechanics.

Email:

mw2319@bath.ac.uk

Office:

4W 1.12

Papers and preprints

Also see profiles on arXiv, MathSciNet, Google Scholar, ORCID.

[1]

J Dávila, M del Pino, M Musso, and MH Wheeler, Overhanging solitary water waves, submitted. arxiv (93 pages)

[2]

RM Chen, K Varholm, S Walsh, and MH Wheeler, Vortex-carrying solitary gravity waves of large amplitude, submitted. arxiv (38 pages)

[3]

RM Chen, S Walsh, and MH Wheeler, Desingularization and global continuation for hollow vortices, submitted. arxiv (49 pages)

[4]

RM Chen, S Walsh, and MH Wheeler, Global bifurcation for monotone fronts of elliptic equations, J. Eur. Math. Soc. (JEMS), 2024. arxiv (79 pages)

[5]

J Sewell, K Matthies, and MH Wheeler, Solitary solutions to the steady Euler equations with piecewise constant vorticity in a channel, J. Differential Equations 400:376, 2024. arxiv (47 pages)

[6]

RM Chen, L Fan, S Walsh, and MH Wheeler, Rigidity of three-dimensional internal waves with constant vorticity, J. Math. Fluid Mech. 25:71, 2023. arxiv (13 pages)

[7]

SV Haziot and MH Wheeler, Large-amplitude steady solitary water waves with constant vorticity, Arch. Rational Mech. Anal. 247:27, 2023. arxiv (49 pages)

[8] (1,2)

SV Haziot, VM Hur, WA Strauss, JF Toland, E Wahlén, S Walsh, and MH Wheeler, Traveling water waves — the ebb and flow of two centuries, Quart. Appl. Math. 80:317, 2022. arxiv (85 pages)

[9]

VM Hur and MH Wheeler, Overhanging and touching waves in constant vorticity flows, J. Differential Equations 338:572, 2022. arxiv (19 pages)

[10]

Z Hassainia and MH Wheeler, Multipole vortex patch equilibria for active scalar equations, SIAM J. Math. Anal. 54(6):6054, 2022. arxiv (42 pages)

[11]

MA Johnson, T Truong, and MH Wheeler, Solitary waves in a Whitham equation with small surface tension, Stud. Appl. Math. 148(2):773, 2022. arxiv (40 pages)

[12]

T Truong, E Wahlén, and MH Wheeler, Global bifurcation of solitary waves for the Whitham equation, Math. Ann. 383:1521, 2022. arxiv (45 pages)

[13]

RM Chen, S Walsh, and MH Wheeler, Center manifolds without a phase space for quasilinear problems in elasticity, biology, and hydrodynamics, Nonlinearity 35(4):1927, 2022. arxiv (59 pages)

[14]

VS Krishnamurthy, MH Wheeler, DG Crowdy, and A Constantin, Liouville chains: new hybrid vortex equilibria of the 2D Euler equation, J. Fluid Mech. 921:A1, 2021. arxiv (35 pages)

[15]

RM Chen, S Walsh, and MH Wheeler, Global bifurcation of anti-plane shear fronts, J. Nonlinear Sci. 31:28, 2021. arxiv (31 pages)

[16]

A Constantin, DG Crowdy, VS Krishnamurthy, and MH Wheeler, Stuart-type polar vortices on a rotating sphere, Discrete Contin. Dyn. Syst. 41(1):201, 2021. (15 pages)

[17]

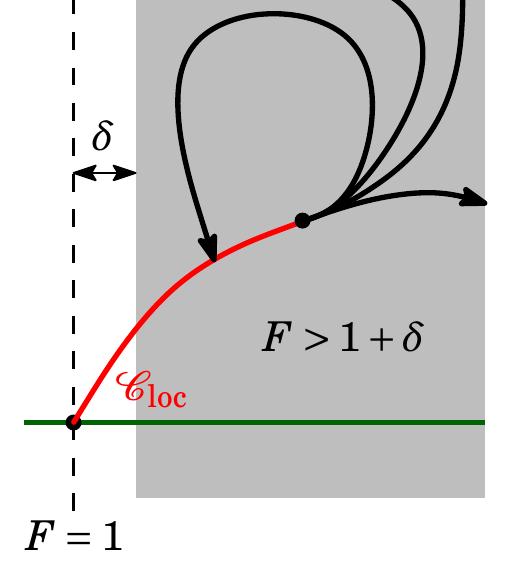
V Kozlov, E Lokharu, and MH Wheeler, Nonexistence of subcritical solitary waves, Arch. Rational Mech. Anal. 241:535, 2021. arxiv (18 pages)

[18]

RM Chen, S Walsh, and MH Wheeler, Large-amplitude internal fronts in two-fluid systems, C. R. Math. Acad. Sci. Paris 358(9-10):1073, 2020. (11 pages)

[19]

VS Krishnamurthy, MH Wheeler, DG Crowdy, and A Constantin, A transformation between stationary point vortex equilibria, Proc. R. Soc. A. 476:20200310, 2020. postprint (21 pages)

[20]

VM Hur and MH Wheeler, Exact free surfaces in constant vorticity flows, J. Fluid Mech. (Rapids) 896:R1, 2020. postprint (10 pages)

[21]

Z Hassainia, N Masmoudi, and MH Wheeler, Global bifurcation of rotating vortex patches, Comm. Pure Appl. Math. 73(9):1933, 2020. arxiv (48 pages)

[22]

VS Krishnamurthy, MH Wheeler, DG Crowdy, and A Constantin, Steady point vortex pair in a field of Stuart-type vorticity, J. Fluid Mech. (Rapids) 874:R1, 2019. preprint (11 pages)

[23]

MH Wheeler, On stratified water waves with critical layers and Coriolis forces, Discrete Contin. Dyn. Syst. 39(8):4747, 2019. preprint (24 pages)

[24]

RM Chen, S Walsh, and MH Wheeler, Existence, nonexistence, and asymptotics of deep water solitary waves with localized vorticity, Arch. Rational Mech. Anal. 234(2):595, 2019 arxiv (39 pages)

[25]

MH Wheeler, Simplified Models for Equatorial Waves with Vertical Structure, Oceanography 31(3):36, 2018. (6 pages)

[26]

MH Wheeler, Integral and asymptotic properties of solitary waves in deep water, Comm. Pure Appl. Math. 71: 1941, 2018. preprint, arxiv (16 pages)

[27]

RM Chen, S Walsh, and MH Wheeler, Existence and qualitative theory for stratified solitary water waves, Ann. Inst. H. Poincaré Anal. Non Linéaire 35(2):517, 2017. arxiv (62 pages)

[28]

RM Chen, S Walsh, and MH Wheeler, On the existence and qualitative theory for stratified solitary water waves, C. R. Math. Acad. Sci. Paris 354(6):601, 2016. (5 pages)

[29]

WA Strauss and MH Wheeler, Bound on the slope of steady water waves with favorable vorticity, Arch. Rational Mech. Anal. 222:1555, 2016. preprint, arxiv (26 pages)

[30]

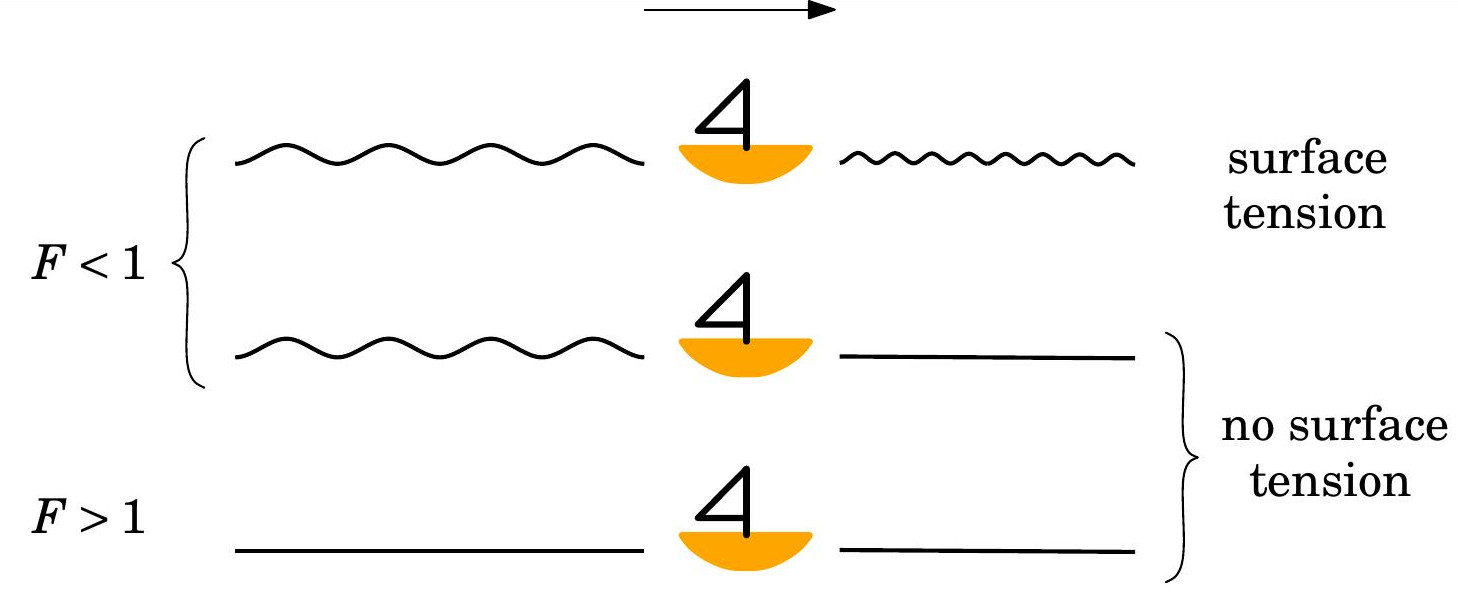
MH Wheeler, The Froude number for solitary water waves with vorticity, J. Fluid Mech. 768:91, 2015. arxiv (22 pages)

[31]

MH Wheeler, Solitary water waves of large amplitude generated by surface pressure, Arch. Rational Mech. Anal. 218(2):1131, 2015. preprint (57 pages)

[32]

MH Wheeler, Large-amplitude solitary water waves with vorticity. SIAM J. Math. Anal. 45(5):2937, 2013. preprint (58 pages)

[33]

S Constantin, RS Strichartz, and M Wheeler, Analysis of the Laplacian and spectral operators on the Vicsek set Commun. Pure Appl. Anal. 10(1):1, 2011. arxiv, website (44 pages)

Expository notes and talks

For a more accessible introduction to the sort of work I do, see this expository talk on solitary waves and fronts (and Section 5 of [8]), or this short introduction to local and global bifurcation theory. The talk is from a series on steady water waves in the ONEPAS seminar, and the notes are from a 2019 lecture to a group of masters students in mathematics and physics.

Teaching

For a full list of past teaching see my CV. Recent teaching:

• Theory of Partial Differential Equations (Spring 2020, 2021, 2022, 2023, 2024).

• Advanced Real Analysis (Fall 2020, 2021, 2022, 2023, 2024).

• Specialist Reading Course “Generalised Solitary Waves in Fourth Order ODEs” (Spring 2022).

• Topics in analysis: fluid mechanics (University of Vienna, Winter 2018).

David Lowry-Duda and I wrote an expository paper aimed at undergraduates which appeared in the American Mathematical Monthly and won an award from the MAA.

PhD students

• Jonathan Sewell (with Karsten Matthies and Alex Doak)

• Daniel Abraham

CV

Last updated November 2024

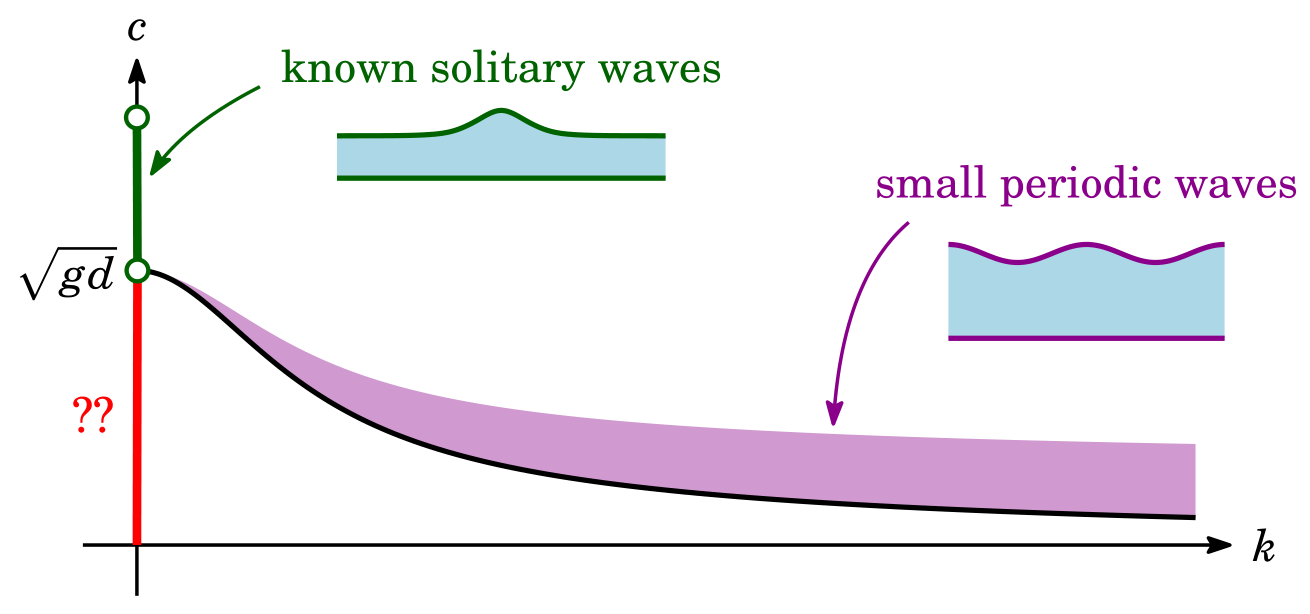
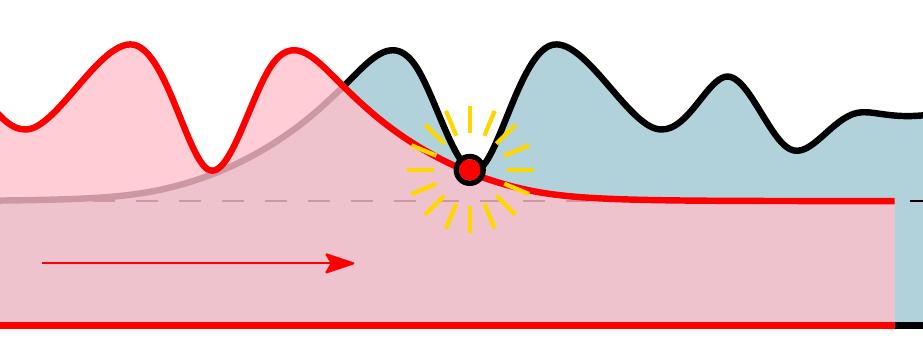
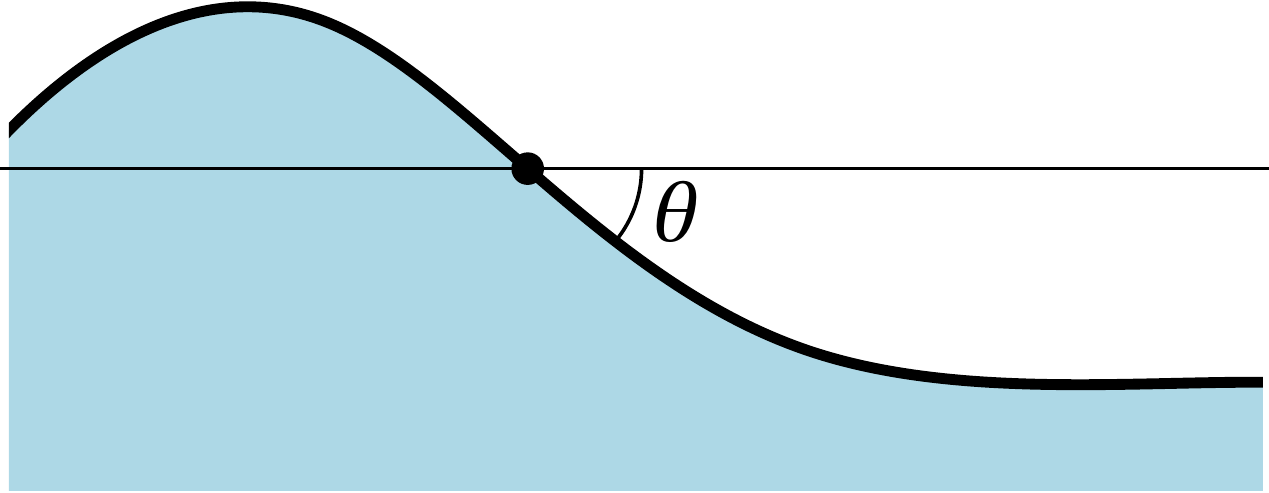
Some figures (mostly from talks)

The gluing procedure in [1].

A wave-borne point vortex in [2].

Hollow vortices in [3].

Large-amplitude bores in [4] and [18].

An overturning solitary wave in [7].

A generalized solitary wave solution of the Whitham equation in [11].

Simple mechanical analogy for solitary waves and bores in the survey [8].

Speed of solitary waves compared to small periodic waves; see [17] and [30].

Explicit overturning waves with constant vorticity in [20]; also see [9].

An extreme solitary wave solution of the Whitham equation in [12].

An anti-plane shear front in [15], with a graph of its centerline.

Streamlines for a hybrid vortex equilibria in [22] and [14]; also see [16].

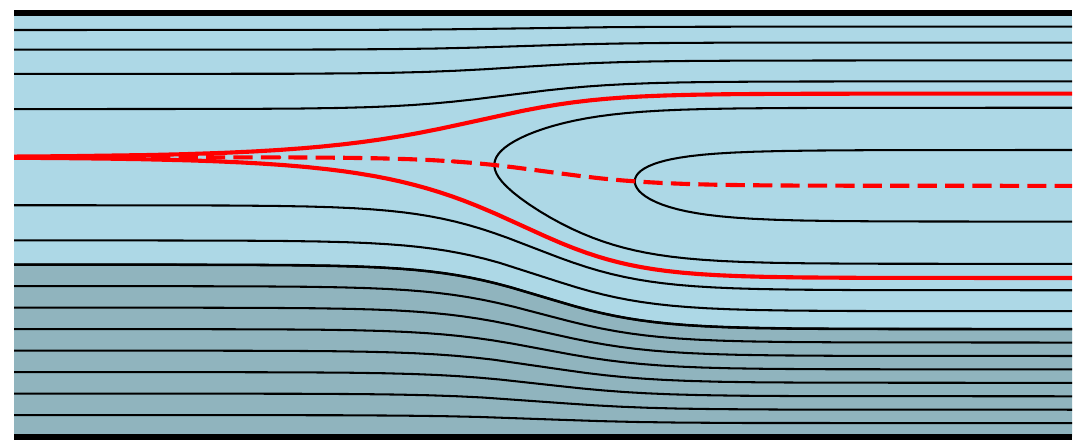
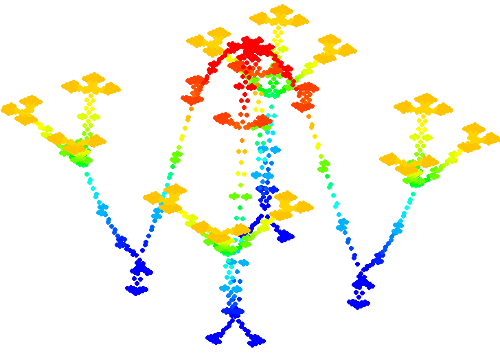
A family of point vortex equilibria which “collapses” in [19]. Also see the August 2020 cover of Proceedings of the Royal Society A!

Bore with a critical layer in [13].

An integration by parts argument in [26] and [24]

A moving planes argument in [27] (also see [28]).

The angle \(θ\) considered in [29]

Waves with localized pressure forcing, see [31].

Vortex patch with streamlines from [21] (also see [10]). See here for more plots.

Constructing the global continuum in [32].

Waves with multiple fluid layers in [23], [25], and [6].

Eigenfunction of the Laplacian on the Vicsek set in [33].